空间音频是什么?
空间音频很多地方也叫做三维音频,它源于我们人据有分辨声音来源方向的能力。虽然一直是比较冷门的研究方向,但在VR的发展下,空间音频也火了一把,很大程度是因为空间音频在在VR的应用所讲究的沉浸感中扮演着极为重要的作用,当声音的方向与画面不匹配的时候,沉浸感会荡然无存,所以高品质的空间音频也成为了VR研究中很重要的一环。

https://developers.google.com/resonance-audio/discover/overview
HOA?
HOA 全称是 Higher Order Ambisonics,强硬的翻译的话就是高次混响。它最初的目的是要重建空间中声场的分布。我们可以想象一个空间中的一个球面,我们在球的中心,那么从球外传来的声音会在这个球面上有一个投影,这让我们想到,我们可以把球面以外的声音都无视掉,并假设声源分布在这个球面上。用球面上的声源产生的声场来拟合原来生源产生的声场。HOA就是一个这样去拟合声场的方法。

https://developers.google.com/resonance-audio/discover/concepts
相关知识
球面调和函数 Spherical harmonics
球面调和函数也叫球谐函数,它并不好理解,有机会可以详细的聊一聊,这里只做最最最抽象的介绍,力求知其然不求知其所以然。
这里要做的是类比一下傅里叶变换。我们通常接触的函数都是分布在一维的,每一个 $x$ 对应一个 $f(x)$,我们对 $f(x)$ 进行傅里叶变换会得到 $F(\omega)$。现在我们的目标是一个在球面上分布的函数,我们使用一个球坐标系,球面上的点 $(r,\theta,\phi)$,而对于一个固定大小的球,$r$是一个定值,我们可以暂时只关注$\theta$和$\phi$,那么对于每一组 $(\theta,\phi)$对应一个$f(\theta,\phi)$。傅里叶变换可以将时域信号转化到频域,这样方便我们分析特定频域的信号,对于 $f(\theta,\phi)$,我们只想知道这个函数在空间中一个大概的分布,所以$f(\theta,\phi)$记录的东西无疑太多了,所以我们可以把它转换为 $F_n^m$,这里的 $n$ 和 $m$ 就类似与傅里叶中的 $\omega$。当我们只需要粗略的空间分辨率时,很小的$n$就足够,当需要更精细的空间分辨率时,就需要较大的 $n$ 时的 $F_n^m$,它们会对小的$n$的$F_n^m$的空间的缝隙中进行插值,使空间的分辨率增高。通过球谐分解,我们可以把球面上的函数用更少的数值表达。就如下面这张图,从上至下$n$逐渐增大,对空间的描述能力也逐渐增强。
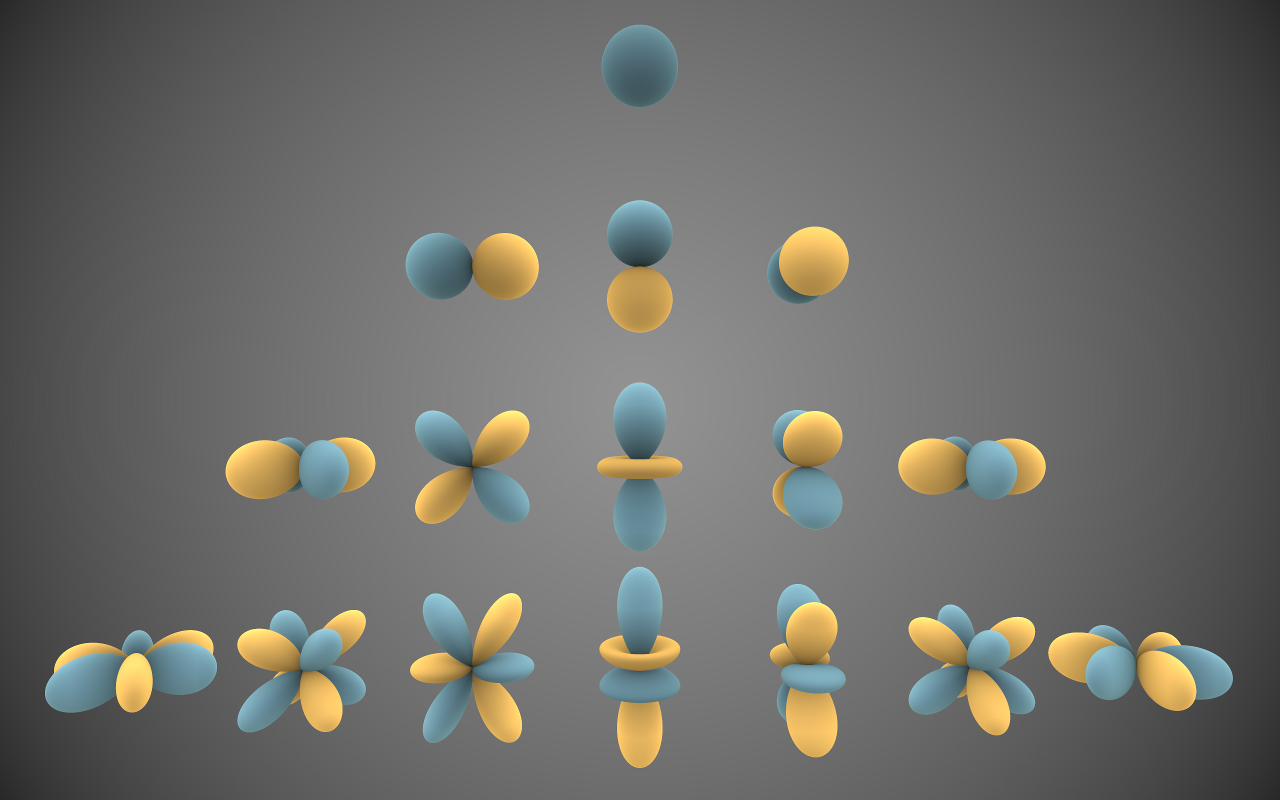
基于球谐函数,球面上的任意函数可以被分解为球谐系数:
$$p(\theta,\phi) = \sum_{n=0}^\infty \sum_{m=-n}^{n} P_n^m Y_n^m(\theta,\phi) $$
声场中方向的信息都被转换到了球谐因子 $Y_n^m(\theta,\phi)$ 中,这个式子看起来是不是也非常像傅里叶变换呢。
球谐贝塞尔函数&汉克尔函数 Spherical Bessel function, Spherical Hanker function
这两个函数的表达式也比较复杂,好在我们通常也不需要记住,只需要知道它门描述了波动方程在球坐标系下的解,它与三个参数有关,对应的上面的球谐函数的阶数 $n$,波的频率球面的半径有关,在之后的数学中我们会用到。贝塞尔函数写作 $j_n(kr)$ 或者 $j_n(\frac{\omega}{c}r)$,$k$是一个波的波数,它等于 $\frac{\omega}{c}$,$\omega$ 表示声音的角频率,$r$表示球面的半径。汉克尔函数类似,但有一类汉克尔函数和二类汉克尔函数,分别表示从内往外传递的出射波和从外往内传播的入射波,写作 $h_n^{(1)}(kr)$ 与 $h_n^{(2)}(kr)$。
格林函数 Green function
格林函数用于描述在开放空间中(没有障碍物没有反射折射)一个声源到空间另外一点的响应。用$\boldsymbol{x_0}$表示声源的位置,声源到$\boldsymbol{x}$点的传达函数为为 $G(\boldsymbol{x}-\boldsymbol{x_0},\omega) = \dfrac{e^{ik|\boldsymbol{x}-\boldsymbol{x_0}|}}{4\pi|\boldsymbol{x}-\boldsymbol{x_0}|}$。$\omega$表示声音的角频率,格林函数同样有在时域上的表达,可以看作是一个延时函数。
HOA!
我们之前说到了,HOA的思路是用一个球面上的音源去拟合球内的声场。我们把这个思想在球坐标系中用公式描述出来。对于一个特定频率的声波(角频率为 $\omega$ )球内一点 $\boldsymbol{x}$,该点的声强是球面$S_0$上声源的在该点的响应的叠加:
$$p(\boldsymbol{x},\omega) = \int_{\Omega_0 \in S_0} D(\boldsymbol{x_0},\omega) G(\boldsymbol{x}-\boldsymbol{x_0},\omega)d\Omega_0$$
这里 $D(\boldsymbol{x_0},\omega)$ 表示了球面分布的声源的驱动信号(driving signal),$\boldsymbol{x_0}$ 则代表着它们对应的坐标。
于此同时,我们也可以对 $p(\boldsymbol{x},\omega)$ 进行球谐分解,把它写作:
$$p(r,\theta,\phi,\omega) = \sum_{n=0}^\infty \sum_{m=-n}^{n} j_n(\frac{\omega}{c}r) P_n^m(\omega) Y_n^m(\theta,\phi)$$
这一步,我们也叫做声场的编码,$p(\boldsymbol{x},\omega)$可以是录音得到的,也可以是仿真生成的。
因为$j_n(\frac{\omega}{c}r)$可能等于0,在某些频率无法得到$P_n^m(\omega)$,这时候就会遇到禁止频率的问题。这也是声场重建中一个比较重要的问题。
同样 $G(\boldsymbol{x}-\boldsymbol{x_0},\omega)$ 也进行对应的球谐变换。如果我们用$L$个扬声器重建声场,那么上面这个式子可以写作
$$p(r,\theta,\phi,\omega) = \sum_{n=0}^\infty \sum_{m=-n}^{n} j_n(\frac{\omega}{c}r) { \sum_{\ell=1}^{L} D_\ell(\boldsymbol{x_0},\omega)G_{nm}^{\ell}(\omega) } Y_n^m(\theta,\phi)$$
$$P_n^m = \boldsymbol{C(\omega)} \cdot \boldsymbol{D(\boldsymbol x_0,\omega)}$$
$$\boldsymbol{C(\omega)} = [G_{nm}^{1}(\omega) \quad G_{nm}^{2}(\omega) \quad \cdots \quad G_{nm}^{L}(\omega)]$$
这样通过求矩阵的逆,我们就可以求得驱动信号$D(\boldsymbol x_0,\omega)$,从而重建声场。这也是HOA的解码。
同时我们也可以避免矩阵的求逆,直接算出驱动函数的解析解。这里就不展开了。

